6. Memorial de cálculos estruturais

Todas as equações utilizadas para os cálculos estruturais foram retiradas do livro "Mecânica dos Materiais" de Beer e Johnston.

6.1. Torque requerido do motor

Para calcular o torque do motor, adotou-se o método de inércia de cargas. Inicialmente, realizou-se a análise da inércia da carga aplicada individualmente em cada esteira, considerando uma carga aproximada de 560g e um diâmetro de rolete de 50mm, considerando o caso mais crítico. Utilizando a Equação 1, apresentada abaixo, obteve-se um valor de 0,00035 kg m².

Em seguida, determinou-se a inércia do rolete com base nos valores tabelados do material utilizado. Considerando aproximados 111g por rolete e dois roletes tracionadores, totalizando 222g, e um diâmetro de 50mm, conforme a Equação 2, encontrou-se um valor de 0,000069375 kg m².

Posteriormente, calculou-se a inércia da cinta, que possui uma massa de 587g. Com a Equação 3, resultou em um valor de 0,00036688 kg m². Para a inércia do motor, recorreu-se aos dados fornecidos pelo fabricante no datasheet comercial disponível online.

Os próximos passos envolveram calcular os momentos totais por meio de um somatório simples e, em seguida, determinar o torque de aceleração. Com base nos dados fornecidos pelo fabricante sobre a velocidade máxima do motor em rad/s e seu tempo de resposta, chegou-se a um valor de 0,0994 N m, que, convertido para kgf cm², resultou em 1,01366427Nm. Esses valores corroboraram com os dados experimentais fornecidos pelo fabricante, servindo como uma validação preliminar dos cálculos realizados até o momento.

O cálculo seguinte envolveu o torque da carga, considerando o peso da carga na esteira e o ângulo de inclinação de 20º em relação ao solo, conforme descrito na Equação 6. Obteve-se um valor de 0.1672 Nm. Somando os torques, chegou-se a um valor final de 0.2665 Nm. Para garantir uma margem de segurança adequada às características da indústria, aplicou-se um fator de segurança de 1,5X a esse torque, resultando em um valor final de 0.3999 Nm. Esse foi o valor de referência seguro para dimensionar os componentes da esteira sujeitos ao torque gerado pelo funcionamento do motor.

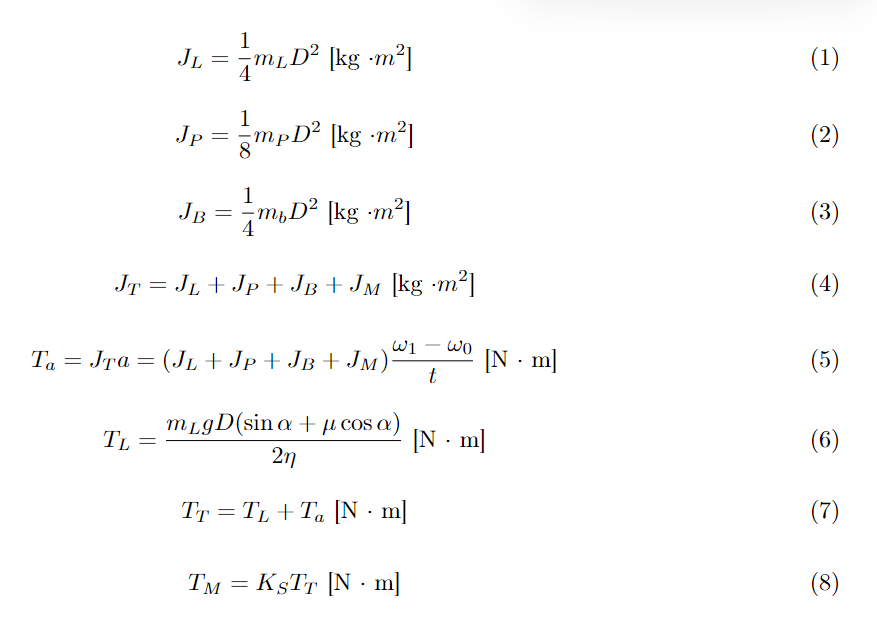
Abaixo, tem-se a Tabela 6.1.1 com os valores encontrados.

Tabela 6.1.1: Valores obtidos

Descrição	Valor
Inércia da carga	0,00035 kg m²
Inércia do rolete	0,000069375 kg m²
Inércia da cinta	0,00036688 kg m²
Inércia total	0,0000048 kg m²
Torque de aceleração	0.09934 Nm
Torque de carga	0.1672 Nm
Torque total	0.2665 Nm
Torque necessário do motor	0.3999 Nm

Fonte: Autoria própria.

6.2. Esforço de tração na correia e na cinta

Para calcular o esforço de tração, requereu-se a avaliação para dois parâmetros de diâmetros distintos, com o intuito de realizar uma verificação inicial relacionada ao diâmetro escolhido para a redução de custos. Dessa forma, consideraram-se os cálculos para os diâmetros de 40mm e 50mm do tubo comercial de PVC.

Para isso, foi necessário levar em consideração o torque total estipulado na seção anterior, dado por 0,2667 N m. Além disso, considerou-se a distância entre os eixos a partir do seu centro, sendo essa distância de 800mm. Levando em conta um coeficiente de atrito de 0,25, foi possível definir as forças relacionadas à tração.

Inicialmente, realizaram-se os cálculos dos ângulos alpha, conforme a Equação 9, e beta, conforme a Equação 10. Nesse caso, esses ângulos não afetaram o sistema apresentado, pois este possui ambos os roletes com o mesmo diâmetro.

Em seguida, calculou-se a força a partir da Equação 11, que considera o torque total já mencionado. Essa força proporcionou o cálculo da força tracionadora, conforme a Equação 12, e a força compressora, conforme a Equação 13. Relacionando essas forças na Equação 14, resultou-se na força total.

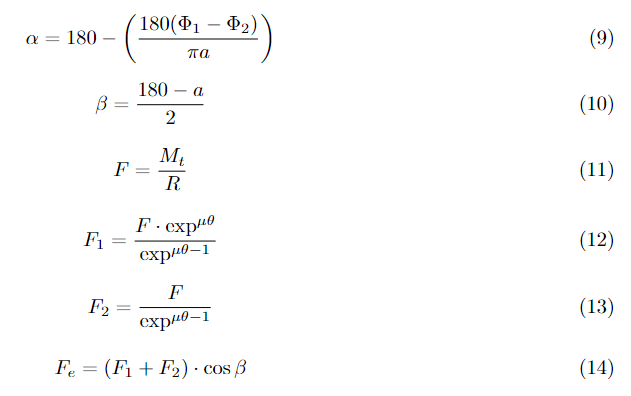
É importante pontuar que o theta se refere ao radiano do alpha que inicialmente é calculado em graus. Abaixo, na Tabela 6.2.1 tem-se o resumo dos resultados.

Tabela 6.2.1: Valores obtidos

Dados	Resultado 50mm	Resultado 40mm
Força	5,334 N	6,6675 N
Força tracionada	9,804 N	12,255 N
Força compressora	4,470 N	5,558 N
Força total	14,274 N	17,843 N

Fonte: Autoria própria.

6.3. Esforços do conjunto rolete e verificação de diâmetro

Para avaliar os esforços do conjunto rolete, utilizou-se como base uma viga engastada com uma carga distribuída no valor da força de tração.

Para solucionar este caso, empregaram-se conceitos simples relacionados às vigas, a partir do cálculo de reações da viga. Inicialmente, realizou-se o equilíbrio de forças com a Equação 15, resultando na Equação 16, onde R1 representa a força de reação vertical e W1 representa a força distribuída.

Considerando uma carga retangular, W1 pode ser dado pela Equação 17. Em seguida, realizou-se o equilíbrio de momentos, dado pelas Equações 18 e 19. Através desses resultados, foi possível obter a segunda força de reação.

Nesse caso, vale ressaltar que a aplicação da força concentrada ocorre no centroide da geometria, no meio da viga, conforme a Equação 20, e com isso foi possível obter R2.

Seguindo com os cálculos, obteve-se a equação de esforço cortante, Equação 21, para essa viga. Para isso, foi feito um corte de seção entre o comprimento da viga, resultando na Equação 22.

Por fim, o cálculo do momento fletor foi realizado seguindo o mesmo princípio do esforço cortante. Dessa forma, obteve-se a Equação 23 e, por meio da análise de uma seção, determinou-se a função do momento fletor descrita pela Equação 24. Considerando a carga retangular, utilizou-se o desdobramento realizado na Equação 25 para finalizar. Abaixo, na Tabela 6.3.1 tem-se o resumo dos resultados.

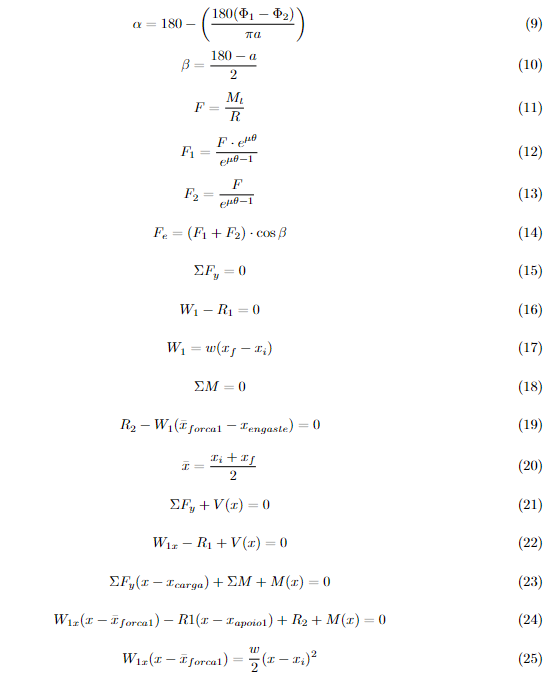
Tabela 6.3.1: Valores obtidos

Dados	Resultado 50mm	Resultado 40mm
Reação vertical	11,4192 N	14,2744 N
Reação de momento	4,5677 Nm	5,7098 Nm
Equação Esforço cortante	-14,274x + 11,4192	-17,843x + 14,843
Equação Momento Fletor	-7,137x² + 11,419x - 4,5677	-8,9215x² + 14,2744x - 5,7098

Fonte: Autoria própria.

Por fim, é possível observar que não há tanta influência nos resultados das duas opções de tubos, tanto os de 40mm quanto os de 50mm de diâmetro. Dessa forma, optou-se pelo de menor custo, que nesse caso é o de 40mm.